Potential Outcome Framework (Rubin's Causal Model)
이전 글 : 2023.02.05 - [Recommender System/Causal Inference] - Causal Inference 인과추론
design based approach의 핵심
- 앞서 작성한 글에서 Design-Based Approach은 treatment를 정의하고 두 가능한 결과를 대조시킴으로써 효과를 추정할 수 있다고 말했다.
- 따라서 연구 대상에 행해질 수 있는 구체적인 처치(treatment)를 정의할 수 없다면 그것의 인과적인 효과나 측정을 정의할 수 없다.
- 인과추론을 위해서 중요한 것은 빅데이터나 복잡한 통계 모형이 아니고 데이터를 모으기 전에 연구자가 얼마나 적절한 연구 디자인을 고안했는지의 여부이다.
Counterfactual and Selection Bias
아래와 같은 문제를 보고자 한다.
"추천 알고리즘 A를 적용하면 사용자의 구매율이 늘어날까?"
실제로 특정 영역에 개인화된 추천 시스템을 도입했고 전체 사용자의 구매율이 늘어났다고 할 때, 우리는 추천 시스템이 사용자의 구매 유도에 영향을 미쳤다고 단정 지을 수 있을까?
마침 사용자가 추천된 상품을 구매하려고 했을 수도 있고 해당 시기에 어떤 이벤트의 발생으로 구매율이 증가했을 수도 있다.
그 외에도 우리가 알지 못하는 여러 외생 변수가 개입하는 환경에서 추천 시스템이 구매율을 유도했다고 보기는 어렵다.
따라서 효과를 추정하는 방법은 아래와 같다.
Causal effect of the treatment =
(1. Actual outcome for treated if treated) - (2. Potential outcome for treated if not treated)
추천 영역이 모든 사용자에게 노출되었다고 가정할때, 우리는 모든 사용자들을 "treatment group(처치 그룹)"으로 보며 노출된 추천 영역은 "treatment(처치)"라고 본다.
동일 시점에 1. treatment group이 treatment를 받았을때의 실제 결과와 2. treatment group이 treatment를 받지 않았을때의 잠재적인 결과의 차이를 비교해본다면 우리는 단지 이 처치에 대한 효과를 추정해볼 수 있다. 이 두 그룹이 가지는 차이는 단지 처치유무 밖에 없기 때문이다.
하지만 현실적으로 동일 그룹에 두 가지의 결괏값을 기대할 순 없다.
따라서 우리는 treatment group에 treatment를 실행하지 않은 결괏값을 실제로 관측할 수 없으며 이것을 Counterfactual(2. potential outcome for treated if not treated)이라고 한다.
- Counterfactuals(반사실) : 만약 알고리즘이 적용되지 않았다면 어떤 결과가 일어났을까?
앞서 말한 것처럼 현실적으로 우리는 counterfactual을 구할 수 없기 때문에 이상적인 방법은 아주 유사한 두 집단(treatment / control group)을 얻어 각각 다른 처치를 적용해 보는 것이다.
하지만 두 집단이 아주 동일한 집단일 순 없기 때문에 필연적으로 selection bias가 발생한다.
- selection bias(선택편향) : Counterfactual과 Control Group의 특성 차이.
Observed effect of the treatment (실험으로 얻어진 결과)
= (Outcome for treatment group) - (Outcome for control group)
= (Outcome for treatment group) [- counterfactual + counterfactual] - (Outcome for control group)
= (Outcome for treatment group) - counterfactual # Causal Effect
+ counterfactual - (Outcome for control group) # Selection Bias
$\text{Causal Effect = (Actual outcome for treated if treated) - (Potential outcome for treated if not treated)} \\ \text{Observe = (Actual outcome for treated if treated) - (Actual outcome for untreated if not treated)}$
따라서 우리는 이 선택 편향을 최대한 줄이는 방향으로 문제를 해결하고자 하며 이는 교란 변수를 통제하는 것과 같다.
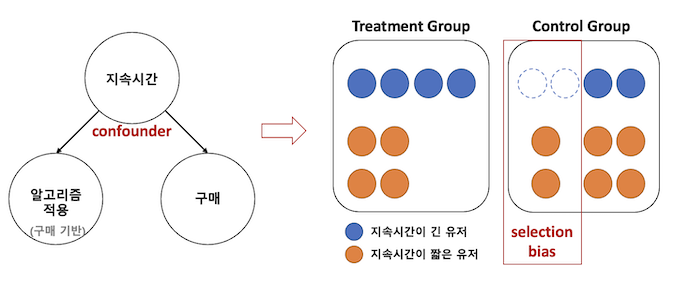
Selection Bias example
반려동물을 키우는 사람(treatment)과 반려동물을 키우지 않는 사람(control)의 우울증 정도의 차이를 비교하는건 유의하지 않다.
일단 반려동물을 키운다는 것은 개인의 자발적인 선택이며 애초에 반려동물을 키우는 조건에서 우리가 보고자 하는 결과 변수(우울증)가 영향을 미치고 있을지도 모른다.
따라서 selection bias를 제거하여 그 외의 특성 변수들이 동일한 두 그룹간의 결과 변수를 비교해야 한다.
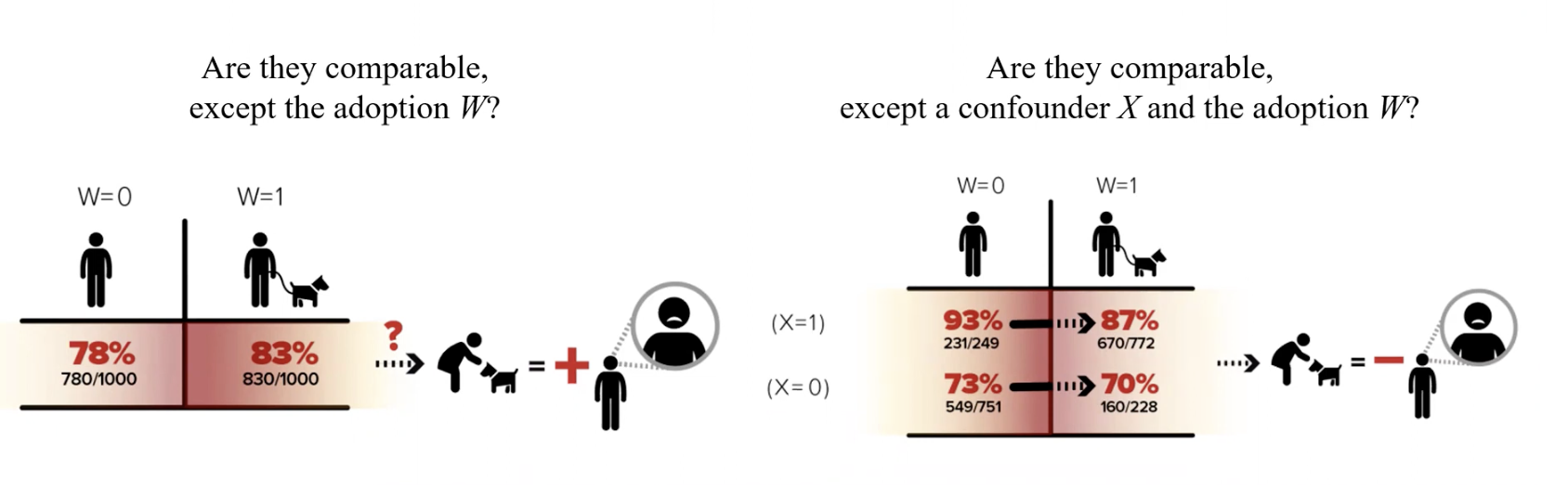
아래 자료에서 왼쪽 그림은 반려동물을 키우는 사람 중 우울한 사람이 83%로 반려동물을 키우지 않는 사람들보다 더 높은 우울증 비율을 보이고 있다. 이 그림에서 우리가 반려동물을 키우면 우울증이 생긴다고 판단하는 것은 옳지 않다.
오른쪽 그림처럼 두 그룹에 영향을 미치는 교란변수 X를 분리하여 결과를 비교해보았을때, 각 조건에서 반려동물을 키우는 것이 우울증의 비율을 낮추는 것에 효과가 있다고 볼 수 잇다.
Estimating Effects on Potential Outcomes
i라는 개인이 받을 수 있는 처치 (Treatment) 유무를 $T_i$라고 하고 개인에 대한 결과를 $Y_i$라고 한다.
$T_i = \begin{cases} 1, \qquad \text{if treated} \\ 0, \qquad \text{if not treated} \end{cases}$
$Y_i = \begin{cases} Y_{1i}, \qquad \text{if} \ T_1 = 1 \\ Y_{0i}, \qquad \text{if} \ T_0 = 0 \end{cases}$
개인에 대한 treatment에 대한 효과는 다음과 같이 얻을 수 있다.
이러한 개인의 효과는 ITE(Individual Treatment Effect)라고 정의한다.
개인의 효과를 모두 구해 평균을 구하면 모든 사용자에 대한 효과를 추정할 수 있다.
$\text{ITE} = Y_{1i} - Y_{0i}$
$\text{Causal Effect} = E[Y_{1i} - Y_{0i}]$
하지만 아래의 그림에서 알 수 있듯이 개인에 대한 관측 결과는 $Y_{1i}$나 $Y_{0i}$ 둘 중 하나만 얻을 수 있기때문에 ITE를 구하는 것은 불가능하다.
이를 식으로 표현하면 다음과 같다.
$Y^{obs} = Y_{1i}T_i + Y_{0i}(1-T_i)$

따라서 개인에 대한 효과를 추정하여 평균을 내는 것이 아니라 Treatment Group과 Control Group의 평균을 구하여 각 그룹의 평균에 따른 차이를 구하는 방법을 사용한다.
이러한 그룹의 평균을 구하여 얻은 효과를 ATE(Average Treatment Effect)라고 정의한다.
$\text{ATE} = E[Y_{1i}|T_i=1] - E[Y_{0i}|T_i=0]$
참조 링크
[Youtube] 인과추론의 데이터과학'Recommender System > Causal Inference' 카테고리의 다른 글
| Causal Inference 인과추론 (1) | 2023.02.05 |
|---|